Hangeul (Korean Alphabet) – the sole writing system in the world whose founder is known

Hunmin Jeongeum: Correct sounds for the instruction of the people

Because most writing systems changed and developed gradually over long periods of time before taking on their current forms, it is unclear by whom or when they were invented. Not so in the case of Hangeul (the Korean writing system), which is the only writing system in the world for which the name of its creator and date of founding are known. This is one reason why many linguistics scholars describe Hangeul as one of the most amazing alphabets ever created.

Hangeul was founded in 1443 A.D. (25th year of King Sejong) by King Sejong the Great (the fourth king of the Joseon Dynasty) and the scholars of Jiphyeonjeon. The title of the book that explains the principles of Hangeul, Hunmin Jeongeum, which literally means "correct sounds for the instruction of the people," was also Hangeul's original name.

<Portrait of King Sejong the Great.>

King Sejong the Great explained in the foreword of Hunmin Jeongeum his purpose for inventing Hangeul as follows: "Because the language of our nation is different from China, there are many among our ignorant people who are unable to express what they wish to say. I took pity on this state of affairs and made 28 letters to correct it." Because there was no Korean writing system at the time, Koreans used the Chinese writing system. As spoken and written Korean were so different, and it was difficult for most to learn the many and complicated Chinese characters, most commoners were illiterate and did not know how to write. Thus, King Sejong the Great invented an alphabet that appropriately reflected the Korean language and was easy to learn, even by the uneducated general public.

<Hunmin Jeongeum Haerye manuscript inscribed on the UNESCO Memory of the World list in 1997.>

While it was clear when and why Hangeul was invented, scholars for years held various theories about its founding principles, since nothing was known about this particular aspect. However, with the discovery of the Hunmin Jeongeum Haerye (a document that supplements the Hunmin Jeongeum) in 1940, the high degree of scientificity on which Hangeul was based was finally revealed. With its foreword and explanation authored by King Sejong himself, Hunmin Jeongeum Haerye is registered as a UNESCO Memory of the World. In honor of King Sejong the Great, the King Sejong Literacy Prize is awarded on September 8 of each year (International Literacy Day) to an individual or organization that has devoted itself to dispelling illiteracy.

<Recipients of the UNESCO King Sejong Literacy Prize pose for a photo in front of the King Sejong statue in Gwanghwamun, Seoul.>

Five consonants based on scientific principles and the shapes of vocal organs

The five basic Hangeul consonants are: ㄱ, ㄴ, ㅁ, ㅅ, and ㅇ. Other letters are made by adding an extra stroke or stacking onto these basic five letters as follows: ㄱ ㅋ ㄲ. Therefore, once one knows the first five letters, the rest are learned with ease. But even these basic five letters don't need to be memorized because they have been created based on the shapes of the parts of the body used to speak. That is: "ㄱ" is the shape of the tongue's root blocking the throat; "ㄴ" is the shape of the tongue touching the upper gums; "ㅁ" is the shape of the open mouth; "ㅅ" is the shape of the teeth; and "ㅇ" is the shape of the opening at the back of the throat.

The most prominent characteristic of Hangeul is the relationship between each individual letter and its sound. For example, the English word "city" is actually closer in pronunciation to "[siri]." The word "gentleman" is pronounced "[ʤénmən]," an indication that the letters t, r and n share sounds due to their being in the same sound group. In English, the pronunciation and shape of each alphabet letter have nothing in common, and therefore must be memorized separately. However, all letters of Hangeul are designed in such a way that similarly pronounced letters also look similar, as in ㄴ, ㄷ, ㅌ and ㄸ (for ㄹ: semi-lingual sound). This highly scientific method is the reason why linguistics scholars around the world are amazed by Hangeul.

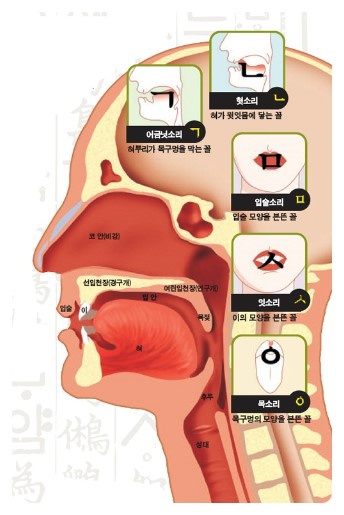
<Hangeul was invented as a scientific interpretation of the human vocal organs.>

All vowels reflect the Eastern philosophy of heaven-Earth-human

At the root of Eastern philosophy is the idea that heaven, Earth, and human are one. Hangeul is also based on this concept. Accordingly, "•" is based on the round shape of the sky, "ㅡ" the flatness of Earth, and "ㅣ" the shape of a person standing. Varying combinations of these three shapes are used to express all Hangeul vowels. For example, the vowel "ㅏ" is a combination of ㅣ and ·. The idea of expressing the complicated Korean vowel system with only a dot and two lines (ㅡ, ㅣ) is pure genius, if not a complete mystery. One scholar even went so far as to point out the scientific superiority of Hangeul as one of the reasons for the rise of Korea as an information technology powerhouse.

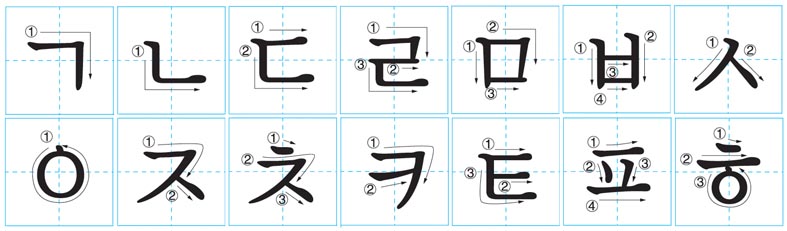
<The order for writing Hangeul consonants – Consonant Table.>

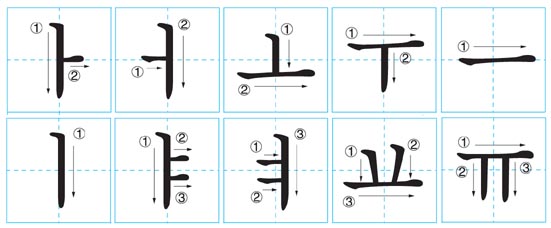
<The order for writing Hangeul vowels – Vowel Table.>

Hangeul, an outstanding intellectual heritage of humanity

The superiority of Hangeul began to be recognized by Western linguists after the 1960s. As stated by Edwin O. Reischauer and J.K. Fairbank of Harvard University in their co-authored book Hangeul in the Prospective of Modern Times: "Hangul is perhaps the most scientific system of writing in general use in any country." Former professor of Leiden University Frits Vos stated of Koreans, "They invented the world's best alphabet!" adding, "It is clear that the Korean alphabet is not only simple and logical, but has, moreover, been constructed in a purely scientific way."

Vos also explains that October 9 is a national holiday in Korea because it was on that day that King Sejong officially promulgated Hangeul. American linguist J.D. McCawley, who wrote the introduction to Vos' thesis, wrote that after October 9 was declared a national holiday, rituals began being held before the portrait of King Sejong complete with tables full of Korean foods like rice cakes.

In his book Writing Systems published in 1985, Professor Geoffrey Sampson of the University of Sussex gives Hangeul a special place in the history of writing by mentioning its "feature system" and asserts that though:"Korea is a fairly small and very distant country … it is a country of great significance for the linguist in two respects. It was in Korea, in the 13c, that the Chinese invention of printing from movable type was first seriously exploited; and in the 15c a Korean created for the use of his countrymen a wholly original and quite remarkable phonographic script, nowadays called Han'gŭl."Sampson concludes his book as follows:"Han'gŭl must unquestionably rank as one of the great intellectual achievements of humankind."

<An essay contest for foreigners in commemoration of Hangeul Day.>

<Various products with Hangeul designs.>